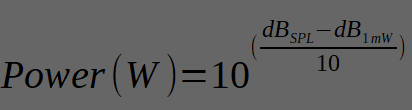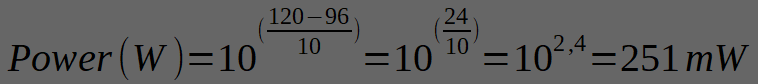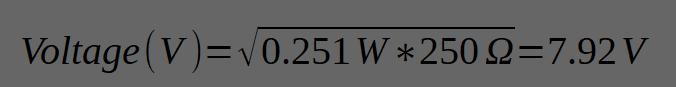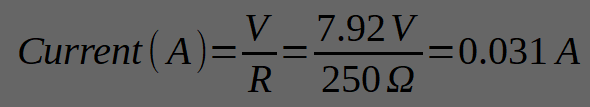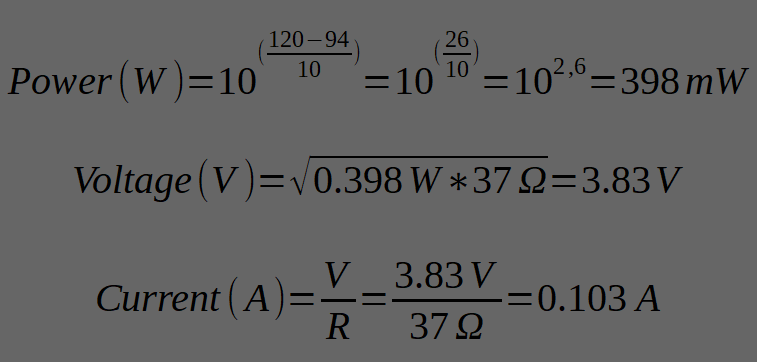This community found a good balance between objective and subjective audiophilia.
And as tubes are somewhat popular on here (most OTL tube amps don’t play well with low impedance headphones), I think most people here know what resistance (and by extension, impedance) is.
Then word it in a way that is understandable?
If my answer relied on pretending to be the smartest person in the room, then I would reconsider the wording of said answer.
Except I did word my original post in an easier to understand way. You came in and complicated it and thought you were smarter by replying in the 101 thread. You literally just did the thing you said you don’t do.
This thread is my attempt at pulling back the magic veil that somehow surrounds everyday devices.
I am nowhere near as good at breaking down big and complex issues into understandable and relatable bits as people like Louis Rossman or Tarah Wheeler when it comes to Right to Repair.
I despise incorrectness in the name of providing a simple answer!
Like I said, explain the problem in an understandable way that does not rely on words to make you seem smart.
Given your reaction, I am not sure if you don’t understand me from a knowledge point or I worded it poorly.
Yes i is dumb. you no hypocrite me sorrrryyyy
Power, Sensitivity and Impedance
For ease of explanation, I will write this for DC circuits. As such I will use resistance and impedance interchangeably. Audio is off course AC.
This part aims to explain how to evaluate if your amplifier can properly drive your speaker or more commonly, headphone. There are some assumptions on my part that I (hopefully) mark clearly.
Units and Vocabulary
In Part 2 of this thread, I touched briefly on Ohm’s Law. Short refresher:
Power (in Watt) is Current (in Ampere) times Voltage (in Volt)
Voltage (V) equals Current (A) times Resistance (Ω), or squre root of Power (W) times Resistance (Ω)
Sensitivity in dB per W (the lower case “m” often found before the W is the metric prefix for 10^-3)
Decibel (the lower case “d” is also a metric prefix, the unit is “Bel”) is used to describe ratios. It is logarithmic meaning for each 10dB you need 10 times the power.
RMS Voltage (Vrms), Peak Voltage(Vpk) and Peak to Peak Voltage (Vpp)
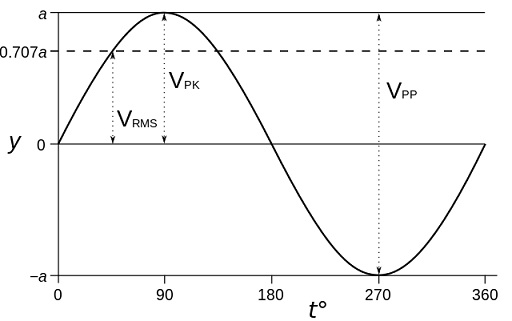
All of these are used to describe voltage in an AC circuit.
Vrms is often described as the equivalent DC voltage after rectifying.
Vrms = Vpk * 1/sqrt(2) ≈ Vpk x 0.707
Vpk ≈ Vrms x 1.4
In practical terms: The USAs normal power outlets deliver 120V RMS. Meaning the peak voltage is 170V
In Europe with its 230V RMS, you get 326V peak voltage.
This is why capacitors on the grid facing side of power supplies are rated for 400V, not 230V.
Calculations
Example for Beyerdynamic DT-990’s (250 Ω, 96dB/mW):
To get a good headroom (pulling from thin air) 120dB SPL, we need
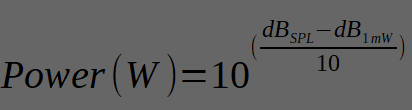
Now we know the required power. To push that power through the headphone, we need a voltage::
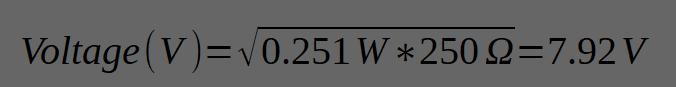
At that voltage, the RMS current (not voltage!) will be:
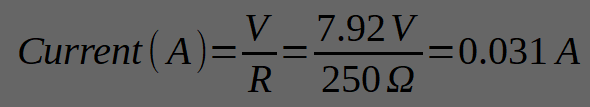
Example for a Hifiman Sundara (37 Ω, 94db/mW):
Why are Planars so inefficent?
Most attraction forces decrease logarithmically, meaning with every unit distance you move away, you only have the square root of the distance in force remaining.
This is way more physics than I am comfortable with, but for the directional force F on a long conductor in a homogenous B-field is equal to the current I times length of the conductor in the field l (lower case L) × B component.
In other words, when you maxed out coil length in the membrane and stregth of the magnets, you need to crank up the current.
Great write up, thank you!
As there is a lot of half-knowledge around this, I think this video (with a quite good explanation) should be here:
If you want any assistance regarding any PCB manufacturing then you can take the help of industrial electronics repair. Hope this helps you.
